[toc]

参考：https://tech.meituan.com/2022/10/13/dive-into-functional-programming-01.html

什么是函数式编程

函数式编程是一种风格范式，没有一个标准的教条式定义。我们来看一下维基百科的定义：

函数式编程是一种编程范式，它将电脑运算视为函数运算，并且避免使用程序状态以及易变对象。其中，λ 演算是该语言最重要的基础。而且 λ 演算的函数可以接受函数作为输入的参数和输出的返回值。

λ 演算

λ 演算（读作 lambda 演算）由数学家阿隆佐·邱奇在 20 世纪 30 年代首次发表，它从数理逻辑（Mathematical logic）中发展而来，使用变量绑定（ binding ）和代换规则（substitution）来研究函数如何抽象化定义（ define ）、函数如何被应用（ apply ）以及递归（recursion）的形式系统。

λ 演算和图灵机等价（图灵完备，作为一种研究语言又很方便）。

通常用这个定义形式来表示一个 λ 演算。

所以 λ 演算式就三个要点：

绑定关系。变量任意性，x、y 和 z 都行，它仅仅是具体数据的代称。
递归定义。λ 项递归定义，M 可以是一个 λ 项。
替换归约。λ 项可应用，空格分隔表示对 M 应用 N，N 可以是一个 λ 项。

演算：变量

实际程序中，通常把绑定变量实现为局部变量或者参数，自由变量实现为全局变量或者环境变量。

演算：代换和归约

Alpha 代换指的是变量的名称是不重要的，在演算过程中它们表示同一个函数。也就是说我们只关心计算的形式，而不关心细节用什么变量去实现。这方便我们不改变运算结果的前提下去修改变量命名，以方便在函数比较复杂的情况下进行化简操作。实际上，连整个 lambda 演算式的名字也是不重要的，我们只需要这种形式的计算，而不在乎这个形式的命名。

Beta 归约指的是如果你有一个函数应用（函数调用），那么你可以对这个函数体中与标识符对应的部分做代换（substitution），方式为使用参数（可能是另一个演算式）去替换标识符。听起来有点绕口，但是它实际上就是函数调用的参数替换。

JS 中的 λ 表达式：箭头函数

一个箭头函数就是一个单纯的运算式，箭头函数我们也可以称为 lambda 函数，它在书写形式上就像是一个 λ 演算式。

// const 语句把表达式x=>x的值输出到标识符id
const id = (x) => x;
console.log(id.name, id.length); // id 1
const x = id;
console.log(x.name, x.length); // id 1 表明name和length是原始引用携带，不因标识符改变和改变

λ 演算是一种抽象的数学表达方式，我们不关心真实的运算情况，我们只关心这种运算形式。

// 定义自然数
const zero = (f) => (x) => f(x);
const one = (f) => (x) => f(f(x));
const two = (f) => (x) => f(f(f(x)));

// ...
// 为了表示函数累计的概念，引入两个辅助函数

// 同一个函数f对x(f f f f x...)执行n次
const times = (n) => (f) =>
  new Array(n).fill(f).reduce((acc, f) => (x) => f(acc(x)));
const countTime = (x) => x + 1;

console.log("COUNT", times(8)(countTime)(0)); // COUNT 8

var SUCC = (n) => (f) => (x) => times(n)(f)(x);
var PLUS = (m) => (n) => (f) => (x) => times(m)(f)(times(n)(f)(x));

console.log("SUCC 4", SUCC(4)(countTime(0))); // SUCC 4 4
console.log("PLUS 4", PLUS(5)(6)(countTime(0))); // SUCC 4 4

我们把 λ 演算中的 f 和 x 分别取为 countTime 和 x，代入运算就得到了我们的自然数。

这也说明了不管你使用符号系统还是 JavaScript 语言，你想要表达的自然数是等价的。这也侧面说明 λ 演算是一种形式上的抽象（和具体语言表述无关的抽象表达）。

函数式编程基础：函数的元、柯里化和 Point-Free

接下来我们将只研究箭头函数，因为它更像是数学意义上的函数（仅执行计算过程）。

没有 arguments 和 this。
不可以被构造 new。

函数的元：完全调用和不完全调用

不论使用何种方式去构造一个函数，这个函数都有两个固定的信息可以获取：

name 表示当前标识符指向的函数的名字。
length 表示当前标识符指向的函数定义时的参数列表长度。

在数学上，我们定义 f(x) = x 是一个一元函数，而 f(x, y) = x + y 是一个二元函数。在 JavaScript 中我们可以使用函数定义时的 length 来定义它的元。

// 一元函数
const one = (a) => a;
// 二元函数
const two = (a, b) => a + b;
// 三元函数
const three = (a, b, c) => a + b + c;

定义函数的元的意义在于，我们可以对函数进行归类，并且可以明确一个函数需要的确切参数个数。函数的元在编译期（类型检查、重载）和运行时（异常处理、动态生成代码）都有重要作用。

如果我给你一个二元函数，你就知道需要传递两个参数。比如+就可以看成是一个二元函数，它的左边接受一个参数，右边接受一个参数，返回它们的和（或字符串连接）。

如果一个二元函数，调用时只使用了一个参数，则返回一个「不完全调用函数」。“不完全调用”在 JavaScript 中也成立。实际上它就是 JavaScript 中闭包（Closure，上面我们已经提到过）产生的原因，一个函数还没有被销毁（调用没有完全结束），你可以在子环境内使用父环境的变量。

多一个元，函数体就多一个状态。如果世界上只有一元函数就好了！我们可以全通过一元函数和不完全调用来生成新的函数处理新的问题。

认识到函数是有元的，这是函数式编程的重要一步，多一个元就多一种复杂度。

柯里化函数：函数元降维技术

柯里化（curry）函数是一种把函数的元降维的技术，这个名词是为了纪念我们上文提到的数学家阿隆佐·邱奇。

首先，函数的几种写法是等价的（最终计算结果一致）。

const add = (a, b) => a + b;
const add = (a) => (b) => a + b;

这里列一个简单的把普通函数变为柯里化函数的方式（柯里化函数 Curry）。

const curry = function (fn) {
  // bind fn
  let length = fn.length; // bind length
  let params = []; // bind params

  return function partial(x) {
    params.push(x); // use params
    if (params.length === length) {
      // use length
      return fn(...params); // use fn
    } else {
      return partial;
    }
  };
};

const curryAdd = curry((a, b, c) => a + b + c);
curryAdd(1)(2)(3); // 6

柯里化函数帮助我们把一个多元函数变成一个不完全调用，利用 Closure 的魔法，把函数调用变成延迟的偏函数(不完全调用函数)调用。这在函数组合、复用等场景非常有用。

虽然你可以用其他闭包方式来实现函数的延迟调用，但 Curry 函数绝对是其中形式最美的几种方式之一。

Point-Free ｜无参风格：函数的高阶组合

函数式编程中有一种 Point-Free 风格，中文语境大概可以把 point 认为是参数点，对应 λ 演算中的函数应用（Function Apply ），或者 JavaScript 中的函数调用（Function Call），所以可以理解 Point-Free 就指的是无参调用。

来看一个日常的例子，把二进制数据转换为八进制数据：

var strNums = ["01", "10", "11", "1110"];

strNums.map((x) => parseInt(x, 2)).map((x) => x.toString(8)); // ['1', '2', '3', '16']

这段代码运行起来没有问题，但我们为了处理这个转换，需要了解 parseInt(x, 2) 和 toString(8) 这两个函数（为什么有魔法数字 2 和魔法数字 8），并且要关心数据（函数类型 a -> b）在每个节点的形态（关心数据的流向）。有没有一种方式，可以让我们只关心入参和出参，不关心数据流动过程呢？

const toBinary = (x) => parseInt(x, 2);
const toString0x = (x) => x.toString(8);
const pipe =
  (...fns) =>
  (x) =>
    fns.reduce((acc, fn) => fn(acc), x);

var strNums = ["01", "10", "11", "1110"];
strNums.map(pipe(toBinary, toString0x)); // ['1', '2', '3', '16']

上面的方法假设我们已经有了一些基础函数 toBinary（语义化，消除魔法数字 2）和 toStringOx（语义化，消除魔法数字 8），并且有一种方式（ pipe ）把基础函数组合（Composition）起来。

如果用 Typescript 表示我们的数据流动就是：

type toBinary = (strNum: string) => number;
type toString0x = (number: number) => string;

type pipe = (
  strNum: string
) => (handler1: toBinary, handler2: toString0x) => returnType<toString>;

pipe 就像一个盒子。BOX 内容不需要我们理解。而为了达成这个目的，我们需要做这些事：

utils 一些特定的工具函数。
curry 柯里化并使得函数可以被复用。
composition 一个组合函数，像胶水一样粘合所有的操作。
name 给每个函数定义一个见名知意的名字。

综上，Point-Free 风格是粘合一些基础函数，最终让我们的数据操作不再关心中间态的方式。这是函数式编程，或者说函数式编程语言中我们会一直遇到的风格，表明我们的基础函数是值得信赖的，我们仅关心数据转换这种形式，而不是过程。

可以说函数式编程范式就是在不停地组合函数。

函数式编程特性

说了这么久，都是在讲函数，那么究竟什么是函数式编程呢？在网上你可以看到很多定义，但大都离不开这些特性。

First Class 函数：函数可以被应用，也可以被当作数据。
Pure 纯函数，无副作用：任意时刻以相同参数调用函数任意次数得到的结果都一样。
Referential Transparency 引用透明：可以被表达式替代。
Expression 基于表达式：表达式可以被计算，促进数据流动，状态声明就像是一个暂停，好像数据到这里就会停滞了一下。
Immutable 不可变性：参数不可被修改、变量不可被修改—宁可牺牲性能，也要产生新的数据（ Rust 内存模型例外）。
High Order Function 大量使用高阶函数：变量存储、闭包应用、函数高度可组合。
Curry 柯里化：对函数进行降维，方便进行组合。
Composition 函数组合：将多个单函数进行组合，像流水线一样工作。

另外还有一些特性，有的会提到，有的一笔带过，但实际也是一个特性。

Type Inference 类型推导：如果无法确定数据的类型，那函数怎么去组合？（常见，但非必需）
Lazy Evaluation 惰性求值：函数天然就是一个执行环境，惰性求值是很自然的选择。
Side Effect IO：一种类型，用于处理副作用。一个不能执行打印文字、修改文件等操作的程序，是没有意义的，总要有位置处理副作用。（边缘）

数学上，我们定义函数为集合 A 到集合 B 的映射。在函数式编程中，我们也是这么认为的。函数就是把数据从某种形态映射到另一种形态。

First Class：函数也是一种数据

函数本身也是数据的一种，可以是参数，也可以是返回值。

通过这种方式，我们可以让函数作为一种可以保存状态的值进行流动，也可以充分利用不完全调用函数来进行函数组合。把函数作为数据，实际上就让我们有能力获取函数内部的状态，这样也产生了闭包。但函数式编程不强调状态，大部分情况下，我们的“状态”就是一个函数的元（我们从元获取外部状态）。

纯函数：无状态的世界

通常我们定义输入输出（IO）是不纯的，因为 IO 操作不仅操作了数据，还操作了这个数据范畴外部的世界，比如打印、播放声音、修改变量状态、网络请求等。这些操作并不是说对程序造成了破坏，相反，一个完整的程序一定是需要它们的，不然我们的所有计算都将毫无意义。

但纯函数是可预测的，引用透明的，我们希望代码中更多地出现纯函数式的代码，这样的代码可以被预测，可以被表达式替换，而更多地把 IO 操作放到一个统一的位置做处理。

const add = async (x) => (await fetch()) + x;

add(1).then(console.log);

这个 add 函数是不纯的，但我们把副作用都放到它里面了。任意使用这个 add 函数的位置，都将变成不纯的（就像是 async/await 的传递性一样）。需要说明的是抛开实际应用来谈论函数的纯粹性是毫无意义的，我们的程序需要和终端、网络等设备进行交互，不然一个计算的运行结果将毫无意义。但对于函数的元来说，这种纯粹性就很有意义。如果一个函数的调用不去控制自己的纯粹性，对别人来说，可能会造成毁灭性打击。因此我们需要对引用值特别小心。

函数的纯粹性要求我们时刻提醒自己降低状态数量，把变化留在函数外部。

引用透明：代换

通过表达式替代（也就是 λ 演算中讲的归约），可以得到最终数据形态。

const add = (a) => (b) => a + b;

const four = add(1)(3); // four = 1 + 3;

也就是说，调用一个函数的位置，我们可以使用函数的调用结果来替代此函数调用，产生的结果不变。

一个引用透明的函数调用链永远是可以被合并式代换的。

不可变性：把简单留给自己

一个函数不应该去改变原有的引用值，避免对运算的其他部分造成影响。

一个充满变化的世界是混沌的，在函数式编程世界，我们需要强调参数和值的不可变性，甚至在很多时候我们可以为了不改变原来的引用值，牺牲性能以产生新的对象来进行运算。牺牲一部分性能来保证我们程序的每个部分都是可预测的，任意一个对象从创建到消失，它的值应该是固定的。

一个元如果是引用值，请使用一个副本（克隆、复制、替代等方式）来得到状态变更。

高阶：函数抽象和组合

高阶函数实际上为我们提供了注入环境变量（或者说绑定环境变量）提供了更多可能。一个高阶函数就是使用或者产生另一个函数的函数。高阶函数是函数组合（Composition）的一种方式。

高阶函数让我们可以更好地组合业务。常见的高阶函数有：

map
compose
fold
pipe
curry
...

惰性计算：降低运行时开销

惰性计算的含义就是在真正调用到的时候才执行，中间步骤不真实执行程序。这样可以让我们在运行时创建很多基础函数，但并不影响实际业务运行速度，唯有业务代码真实调用时才产生开销。

惰性计算让我们可以无限使用函数组合，在写这些函数组合的过程中并不产生调用。但这种形式，可能会有一个严重的问题，那就是产生一个非常长的调用栈，而虚拟机或者解释器的函数调用栈一般都是有上限的，比如 2000 个，超过这个限制，函数调用就会栈溢出。虽然函数调用栈过长会引起这个严重的问题，但这个问题其实不是函数式语言设计的逻辑问题，因为调用栈溢出的问题在任何设计不良的程序中都有可能出现，惰性计算只是利用了函数调用栈的特性，而不是一种缺陷。

记住，任何时候我们都可以重构代码，通过良好的设计来解决栈溢出的问题。

类型推导

没有类型推导的函数式编程，在使用的时候会很不方便，所有的工具函数都要查表查示例，开发中效率会比较低下，也容易造成错误。

但并不是说一门函数式语言必须要类型推导，这不是强制的。像 Lisp 就没有强制类型推导，JavaScript 也没有强制的类型推导，这不影响他们的成功。只是说，有了类型推导，我们的编译器可以在编译器期间提前捕获错误，甚至在编译之前，写代码的时候就可以发现错误。类型推导是一些语言强调的优秀特性，它确实可以帮助我们提前发现更多的代码问题。像 Rust 、Haskell 等。

其他

函数式有很多基础的特性，熟练地使用这些特性，并加以巧妙地组合，就形成了我们的“函数式编程范式”。这些基础特性让我们对待一个 function，更多地看作函数，而不是一个方法。在许多场景下，使用这种范式进行编程，就像是在做数学推导（或者说是类型推导），它让我们像学习数学一样，把一个个复杂的问题简单化，再进行累加/累积，从而得到结果。

同时，函数式编程还有一块大的领域需要进入，即副作用处理。不处理副作用的程序是毫无意义的（仅在内存中进行计算）。

副作用处理：单子 Monad，一种不可避免的抽象

如何去处理 IO 操作？

我们的代码经常在和副作用打交道，如果要满足纯函数的要求，几乎连一个需求都完成不了。实际上，函数式编程语言把副作用包裹到一个特殊的函数里面。

如果一个函数既包含了我们的值，又封装了值的统一操作，使得我们可以在它限定的范围内进行任意运算，那么，我们称这种函数类型为 Monad。Monad 是一种高级别的思维抽象。

什么是 Monad？

先思考一个问题，下面两个定义有什么区别？

const num1 = 1;

function Num(val) {
  return { val };
}
const num2 = Num(2);

num1 是数字类型，而 num2 是对象类型，这是一个直观的区别。

不过，不仅仅如此。利用类型，我们可以做更多的事。因为作为数字的 num1 是支持加减乘除运算的，而 num2 却不行，必须要把它视为一个对象{val: 2}，并通过属性访问符 num2.val 才能进行计算 num2.val + 2。但我们知道，函数式编程是不能改变状态的，现在为了计算 num2.val 被改变了，这不是我们期望的，并且我们使用属性操作符去读数据，更像是在操作对象，而不是操作函数，这与我们的初衷有所背离。

现在我们把 num2 当作一个独立的数据，并假设存在一个方法 fmap 可以操作这个数据，可能是这样的。

// 对元素执行fn方法，并返回m类型
function fmap(m, fn) {
  return Num(fn(m.val));
}

const addOne = (x) => x + 1;
const num3 = fmap(num2, addOne);

得到的还是对象，但操作通过一个纯函数 addOne 去实现了。

上面这个例子里面的 Num，实际上就是一个最简单的 Monad，而 fmap 是属于 Functor（函子）的概念。我们说函数就是从一个数据到另一个数据的映射，这里的 fmap 就是一个映射函数，在范畴论里面叫做态射。

由于有一个包裹的过程，很多人会把 Monad 看作是一个盒子类型。但 Monad 不仅是一个盒子的概念，它还需要满足一些特定的运算规律。

但是我们直接使用数字的加减乘除不行吗？为什么一定要 Monad 类型？

首先，fmap 的目的是把数据从一个类型映射到另一个类型，而 JavaScript 里面的 map 函数实际上就是这个功能。

我们可以认为 Array 就是一个 Monad 实现，map 把 Array< T >类型映射到 Array< K >类型，操作仍然在数组范畴，数组的值被映射为新的值。

type MapType<T, K> = (a: T) => K;

interface Functor<T> {
  fmap: <K>(fn: MapType<T, K>) => Monad<K>;
}

class Monad<T> implements Functor<T> {
  private _value: T;
  constructor(value: T) {
    this._value = value;
  }
  fmap<K>(fn: MapType<T, K>) {
    return new Monad<K>(fn(this._value));
  }
}

const num1 = new Monad(1);
const num2 = num1.fmap((x) => x + 1);

看起来 Monad 只是一个实现了 fmap 的对象（Functor 类型，mappable 接口）而已。但 Monad 类型不仅是一个 Functor，它还有很多其他的工具函数，比如：

bind 函数
flatMap 函数
liftM 函数

这些额外的函数可以帮助我们操作被封装起来的值。

范畴、群、幺半群

范畴论是一种研究抽象数学形式的科学，它把我们的数学世界抽象为两个概念：

对象
态射

为什么说这是一种形式上的抽象呢？因为很多数学的概念都可以被这种形式所描述，比如集合，对集合范畴来说，一个集合就是一个范畴对象，从集合 A 到集合 B 的映射就是集合的态射，再细化一点，整数集合到整数集合的加减乘操作构成了整数集合的态射（除法会产生整数集合无法表示的数字，因此这里排除了除法）。又比如，三角形可以被代数表示，也可以用几何表示、向量表示，从代数表示到几何表示的运算就可以视为三角形范畴的一种态射。

总之，对象描述了一个范畴中的元素，而态射描述了针对这些元素的操作。范畴论不仅可以应用到数学科学里面，在其他科学里面也有一些应用，实际上，范畴论就是我们描述客观世界的一种方式（抽象形式）。

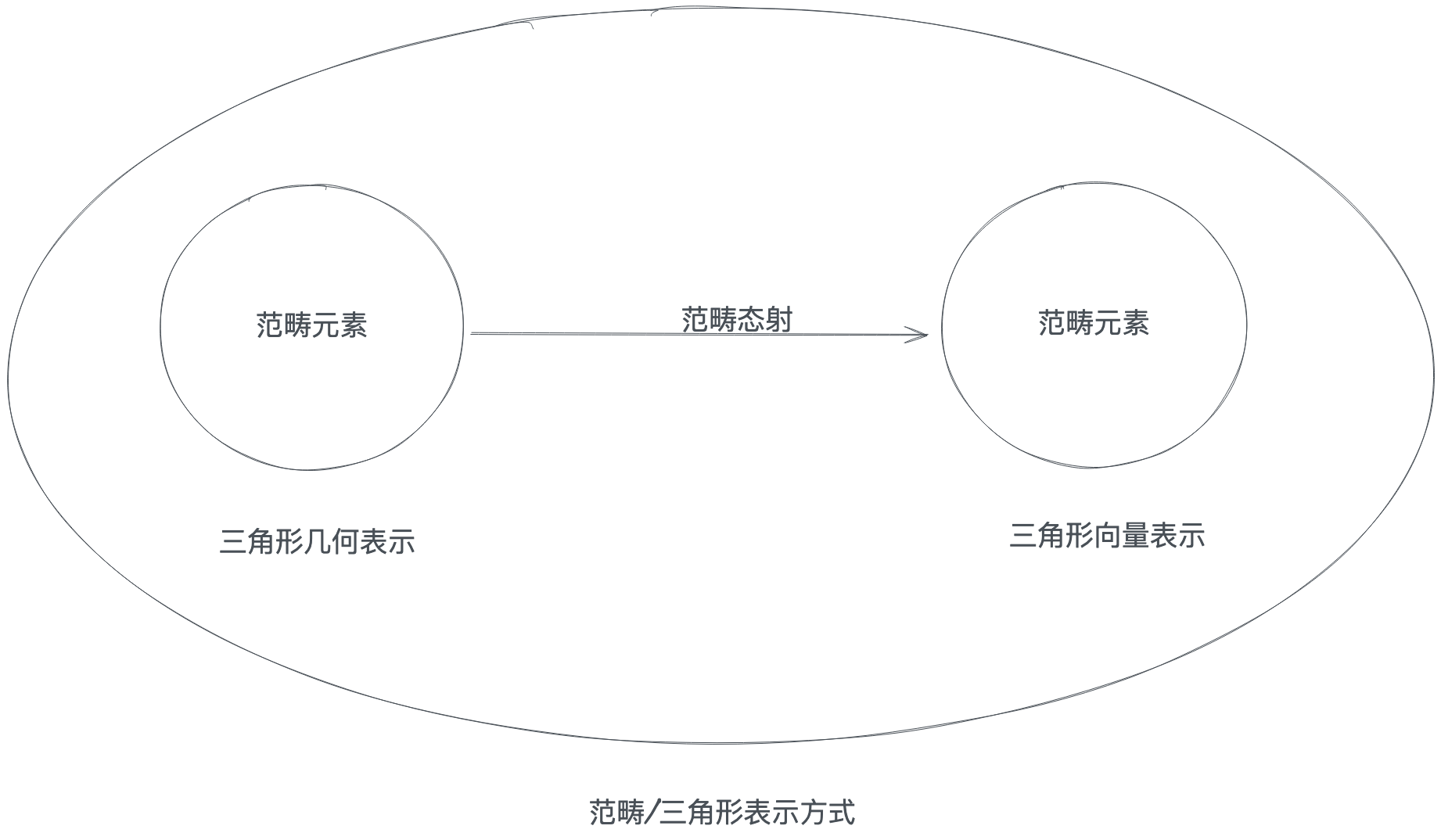
相对应的，函子就是描述一个范畴对象和另一个范畴对象间关系的态射，具体到编程语言中，函子是一个帮助我们映射一个范畴元素（比如 Monad）到另一个范畴元素的函数。

群论（Group）研究的是群这种代数结构，怎么去理解群呢？比如一个三角形有三个顶点 A/B/C，那么我们可以表示一个三角形为 ABC 或者 ACB，三角形还是这个三角形，但是从 ABC 到 ACB 一定是经过了某种变换。这就像范畴论，三角形的表示是范畴对象，而一个三角形的表示变换到另一个形式，就是范畴的态射。而我们说这些三角形表示方式的集合为一个群。群论主要是研究变换关系，群又可以分为很多种类，也有很多规律特性。

科学解释一个 Monad 为自函子范畴上的幺半群。如果没有学习群论和范畴论的话，我们是很难理解这个解释的。

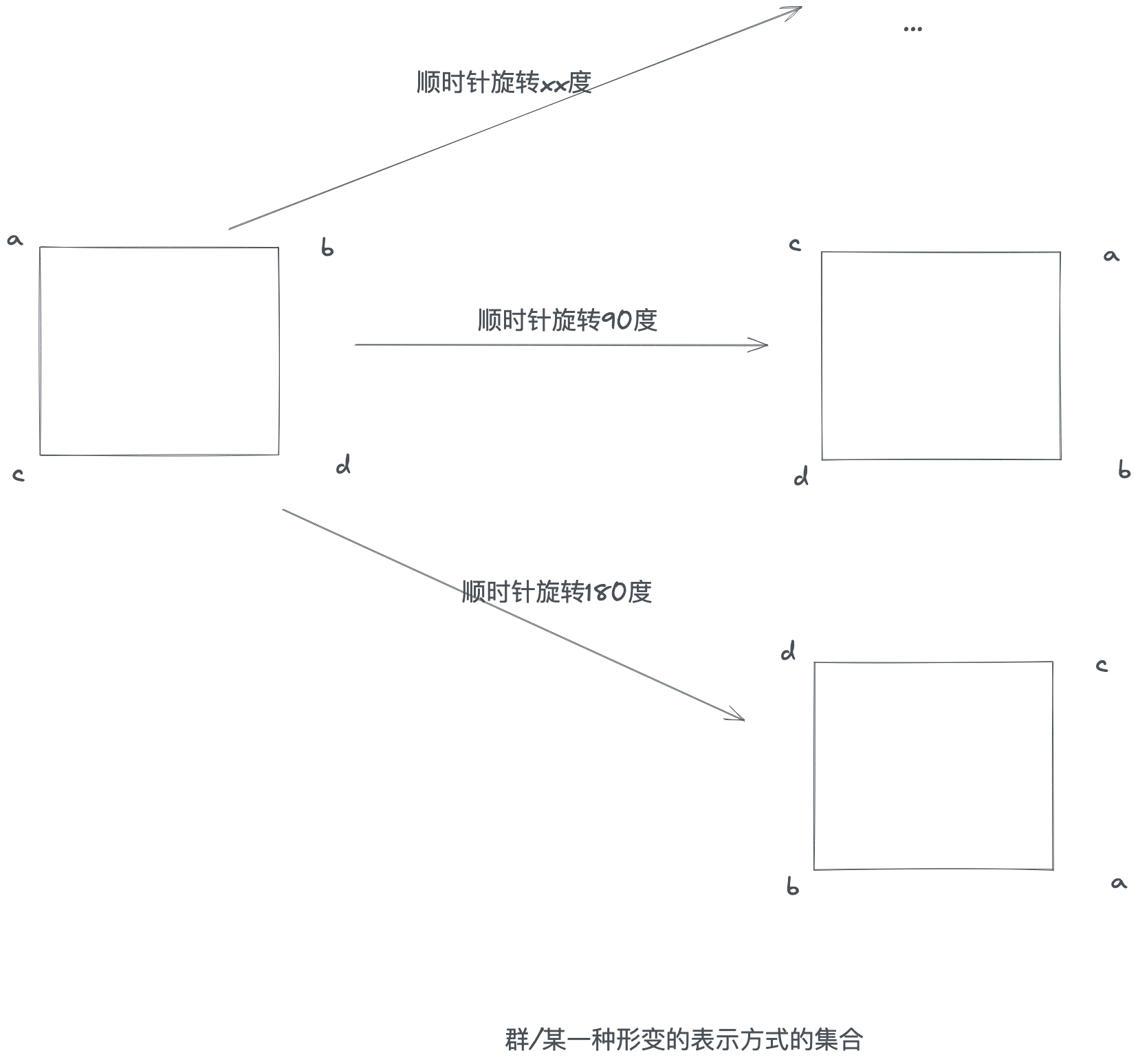
简单来说先固定一个正方形 abcd，它和它的几何变换方式（旋转/逆时针旋转/对称/中心对称等）形成的其他正方形一起构成一个群。从这个角度来说，群研究的事物是同一类，只是性质稍有不一样（态射后）。

另外一个理解群的概念就是自然数（构成一个群）和加法（群的二元运算，且满足结合律，半群）。

到此，我们可以理解 Monad 为：

满足自函子运算（从 A 范畴态射到 A 范畴，fmap 是在自己空间做映射）。
满足含幺半群的结合律。

很多函数式编程里面都会实现一个 Identity 函数，实际就是一个幺元素。比如 JavaScript 中对 Just 满足二元结合律可以这么操作：

function Just(val) {
  return {
    val,
    fmap(fn) {
      return Just(fn(val));
    },
  };
}

function Identity(x) {
  return x;
}

// Just(1).fmap(Identity) == Just(Identity(1))

Monad 范畴：定律、折叠和链

我们要在一个更大的空间上讨论这个范畴对象（Monad）。就像 Number 封装了数字类型，Monad 也封装了一些类型。

// Just 是一个自函子
function Just(__value) {
  return {
    fmap(fn) {
      return Just(fn(__value)); // 态射到Just范畴，自函子
    },
    __inspect() {
      return __value;
    },
  };
}

Monad 需要满足一些定律：

结合律：比如 a · b · c = a · (b · c)。幺元：比如 a · e = e · a = a。

我们可以通过 Monad Just 上挂载的操作来对数据进行计算，这些运算是限定在了 Just 上的，也就是说你只能得到 Just(..)类型。要获取原始数据，可以基于这个定义一个 fold 方法。

const id = (x) => x;
function Just(__value) {
  return {
    fmap(fn) {
      const ret = fn(__value);
      if (ret.fmap) {
        return ret.fmap(id);
      } else {
        return Just(ret);
      }
    },
    fold(fn) {
      const ret = fn(__value);
      if (ret.fold) {
        return ret.fold(id);
      } else {
        return ret;
      }
    },
    isJust() {
      return true;
    },
    isNothing() {
      return false;
    },
  };
}

fold（折叠，对应能力我们称为 foldable）的意义在于你可以将数据从一个特定范畴映射到你的常用范畴，比如面向对象语言的 toString 方法，就是把数据从对象域转换到字符串域。

一旦数据类型被我们锁定在了 Monad 空间（范畴），那我们就可以在这个范畴内连续调用 fmap（或者其他这个空间的函数）来进行值操作，这样我们就可以链式处理我们的数据。

Maybe 和 Either

有了 Just 的概念，我们再来学习一些新的 Monad 概念。比如 Nothing。

function Nothing(val) {
  return {
    fmap(fn) {
      return Nothing();
    },
    fold(fn) {
      return fn(null);
    },
    isJust() {
      return false;
    },
    isNothing() {
      return true;
    },
  };
}

Nothing 表示在 Monad 范畴上没有的值。和 Just 一起正好描述了所有的数据情况，合称为 Maybe，我们的 Maybe Monad 要么是 Just，要么是 Nothing。这有什么意义呢？

其实这就是模拟了其他范畴内的“有”和“无”的概念，方便我们模拟其他编程范式的空值操作。比如：

function add(x, y) {
  return x !== null && y !== null ? x + y : null;
}

这种情况下我们需要去判断 x 和 y 是否为空。在 Monad 空间中，这种情况就很好表示：

function Maybe(val) {
  return {
    fmap(fn) {
      if (val === null) {
        return Nothing();
      } else {
        return Just(val).fmap(fn);
      }
    },
    fold(fn) {
      return fn(val);
    },
  };
}

const addM = (x) => (y) => x.fmap((i) => y.fmap((j) => i + j));

addM(Maybe(1))(Maybe(2)); // Just(3)
addM(Maybe(null))(Maybe(2)); // Nothing

我们在 Monad 空间中消除了烦人的!== null 判断，甚至消除了三元运算符。一切都只有函数。实际使用中一个 Maybe 要么是 Just 要么是 Nothing。因此，这里用 Maybe(..)构造可能让我们难以理解。

如果非要理解的话，可以理解 Maybe 为 Nothing 和 Just 的抽象类，Just 和 Nothing 构成这个抽象类的两个实现。实际在函数式编程语言实现中，Maybe 确实只是一个类型（称为代数类型），具体的一个值有具体类型 Just 或 Nothing，就像数字可以分为有理数和无理数一样。

除了这种值存在与否的判断，我们的程序还有一些分支结构的方式，因此我们来看一下在 Monad 空间中，分支情况怎么去模拟？

function choose(x) {
  if (x) {
    return 1;
  } else {
    return 2;
  }
}

假设我们有一个代数类型 Either，Left 和 Right 分别表示当数据为错误和数据为正确情况下的逻辑。

function Either() {}
Either.from = function (val, [left, right]) {
  if (val.fmap) {
    if (val.isNothing()) {
      return Just(left);
    } else {
      return val.fmap((x) => (x ? right : left));
    }
  } else {
    return Just(val ? right : left);
  }
};

const addOne = (x) => x + 1;
Either.from(true, [1, 2]).fmap(addOne); // Just(3)
Either.from(false, [1, 2]).fmap(addOne); // Just(2)
Either.from(Just(true), [1, 2]).fmap(addOne); // Just(3)
Either.from(Just(false), [1, 2]).fmap(addOne); // Just(2)
Either.from(Nothing(), [1, 2]).fmap(addOne); // Just(2)

这样，我们就可以使用“函数”来替代分支了。这里的 Either 实现比较粗糙，因为 Either 类型应该只在 Monad 空间。这里加入了布尔常量的判断，目的是好理解一些。其他的编程语言特性，在函数式编程中也能找到对应的影子，比如循环结构，我们往往使用函数递归来实现。

IO 的处理方式

终于到 IO 了，如果不能处理好 IO，我们的程序是不健全的。到目前为止，我们的 Monad 都是针对数据的。这句话对也不对，因为函数也是一种数据（函数是第一公民）。我们先让 Monad Just 能存储函数。

function Just(__value) {
  return {
    fmap(fn) {
      const ret = fn(__value);
      if (ret.fmap) {
        return ret.fmap(id);
      } else {
        return Just(ret);
      }
    },
    fold(fn) {
      const ret = fn(__value);
      if (ret.fold) {
        return ret.fold(id);
      } else {
        return ret;
      }
    },
    isJust() {
      return true;
    },
    isNothing() {
      return false;
    },
    apply(monad) {
      if (typeof __value === "function") {
        return monad.fmap(__value);
      } else {
        return Nothing();
      }
    },
  };
}

你可以想象为 Just 增加了一个抽象类实现，这个抽象类为：

interface Applicative<T, K> {
  __value: (v: T) => K;
  apply: (m: Monad<T>) => Monad<K>;
}

这个抽象类我们称为“应用函子”，它可以保存一个函数作为内部值，并且使用 apply 方法可以把这个函数作用到另一个 Monad 上。到这里，我们完全可以把 Monad 之间的各种操作（接口，比如 fmap 和 apply）视为契约，也就是数学上的态射。

现在，如果我们有一个单子叫 IO，并且它有如下表现：

function IO(fn) {
  return {
    fmap(io) {
      return IO(() => io.run(fn));
    },
    fold() {
      return fn;
    },
    apply(io) {
      return io.run(fn);
    },
    run(next = () => {}) {
      next(fn());
    },
  };
}

const one = IO(() => console.log(1));
const two = IO(() => console.log(2));

two.fmap(one).run();
// 1
// 2

我们把这种类型的 Monad 称为 IO，我们在 IO 中处理打印（副作用）。把之前我们学习到的类型合并一下，得到一个示例：

function main() {
  const addOne = (x) => x + 1; // pure function
  const one = Just(1); // monad

  const main = IO(() => {
    const three = Just(addOne).apply(one.fmap(addOne));
    three.fold(console.log); // 3
  });

  main.run();
}

main();

通常一个程序会有一个主入口函数 main，这个 main 函数返回值类型是一个 IO，我们的副作用现在全在 IO 这个范畴下运行，而其他操作，都可以保持纯净（类型运算）。

IO 类型让我们可以在 Monad 空间处理那些烦人的副作用，这个 Monad 类型和 Promise（限定副作用到 Promise 域处理，可链式调用，可用 then 折叠和映射）很像。

总结

函数式编程并不是什么“黑科技”，它已经存在的时间甚至比面向对象编程更久远。

现在我们来回顾先览，实际上，函数式编程也是程序实现方式的一种，它和面向对象是殊途同归的。在函数式语言中，我们要构建一个个小的基础函数，并通过一些通用的流程把他们粘合起来。举个例子，面向对象里面的继承，我在函数式编程中可以使用组合 compose 或者高阶函数 hoc 来实现。

尽管在实现上是等价的，但和面向对象的编程范式对比，函数式编程有很多优点值得大家去尝试。

优点

函数纯净程序有更少的状态量，编码心智负担更小。随着状态量的增加，某些编程范式构建的软件库代码复杂度可能呈几何增长，而函数式编程的状态量都收敛了，对软件复杂度带来的影响更小。
引用透明性可以让你在不影响其他功能的前提下，升级某一个特定功能（一个对象的引用需要改动的话，可能牵一发而动全身）。
高度可组合函数之间复用方便（需要关注的状态量更少），函数的功能升级改造也更容易（高阶组件）。
副作用隔离所有的状态量被收敛到一个盒子（函数）里面处理，关注点更加集中。
代码简洁/流程更清晰通常函数式编程风格的程序，代码量比其他编程风格的少很多，这得益于函数的高度可组合性以及大量的完善的基础函数，简洁性也使得代码更容易维护。
语义化一个个小的函数分别完成一种小的功能，当你需要组合上层能力的时候，基本可以按照函数语义来进行快速组合。
惰性计算被组合的函数只会生成一个更高阶的函数，最后调用时数据才会在函数之间流动。
跨语言统一性不同的语言，似乎都遵从类似的函数式编程范式，比如 Java 8 的 lambda 表达式，Rust 的 collection、匿名函数；而面向对象的实现，不同语言可能千差万别，函数式编程的统一性让你可以舒服地跨语言开发。
关键领域应用因为函数式编程状态少、代码简洁等特点，使得它在交互复杂、安全性要求高的领域有重要的应用，像 Lisp 和 Haskell 就是因上一波人工智能热而火起来的，后来也在- 一些特殊的领域（银行、水利、航空航天等）得到了较大规模的应用。
...

不足

陡峭的学习曲线面向对象和命令式编程范式都是贴近我们的日常习惯的方式，而函数式编程要更抽象一些，要想更好地管理副作用，你可能需要学习很多新的概念（响应式、Monad 等），这些概念入门很难，而且是一个长期积累的过程。
可能的调用栈溢出问题惰性计算在一些电脑或特种程序架构上可能有函数调用栈错误（超长调用链、超长递归），另外许多函数式编程语言需要编译器支持尾递归优化（优化为循环迭代）以得到更好的性能。
额外的抽象负担当程序有大量可变状态、副作用时，用函数式编程可能造成额外的抽象负担，项目开发周期可能会延长，这时可能用其他抽象方式更好（比如 OOP）。
数据不变性的问题为了数据不变，运行时可能会构建生成大量的数据副本，造成时间和空间消耗更大，拖慢性能；同时数据不可变性可能会造成构建一些基础数据结构的时候语法不简洁，性能也更差（比如 LinkedList、HashMap 等数据结构）。
语义化的问题往往为了开发一个功能，去造许多的基础函数，大量业务组件想要语义化的命名，也会带给开发人员很多负担；并且功能抽象能力因人而异，公共函数往往不够公用或者过度设计。
生态问题函数式编程在工业生产领域因其抽象性和性能带来的问题，被许多开发者拒之门外，一些特定功能的解决方案也更小众（相比其他编程范式），生态也一直比较小，这成为一些新的开发人员学习和使用函数式编程的又一个巨大障碍。
...

日常业务开发中，往往我们需要取长补短，在适合的领域用适合的方法/范式。大家只要要记住，软件开发并没有“银弹”。

FAQ

Q：你愿意在生产中使用 Haskell/Lisp/Clojure 等纯函数式语言吗？

A：不论是否愿意使用，现在很多语言都开始引入函数式编程语法了。并不是说函数式编程一定是优秀的，但它至少没有那么恐怖。有一点可以肯定的是，学习函数式编程可以扩展我们的思维，增加我们看问题的角度。

Q：有没有一些可以预见的好处？

A：有的。比如强制你写代码的时候去关注状态量（多少、是否引用值、是否变更等），这或多或少可以帮助你写代码的时候减少状态量的使用，也慢慢地能复合一些状态量，写出更简洁的代码。

Q：函数式编程能给业务带来什么好处？

A：业务拆分的时候，函数式的思维是单向的，我们会通过实现，想到它对应需要的基础组件，并递归地思考下去，功能实现从最小粒度开始，上层逐步通过函数组合来实现。相比于面向对象，这种方式在组合上更方便简洁，更容易把复杂度降低，比如面向对象中可能对象之间的相互引用和调用是没有限制的，这种模式带来的是思考逻辑的时候思维会发散。

这种对比在业务复杂的情况下更加明显，面向对象必须要优秀的设计模式来实现控制代码复杂度增长不那么快，而函数式编程大多数情况下都是单向数据流+基础工具库就减少了大量的复杂度，而且产生的代码更简洁。

函数式编程相关概念整理